СЛОЖЕНИЕ СКОРОСТЕЙ И ДВИЖЕНИЕ С УСКОРЕНИЕМ
Движение в одну сторону
\[\begin{aligned}V_\Sigma = V_{лодки} + V_{реки}
\end{aligned}\]Движение в разные стороны
\[\begin{aligned}V_\Sigma = V_{лодки} - V_{реки}
\end{aligned}\]Перпендикулярное движение
\[\begin{aligned}V_\Sigma = \sqrt{{V}^2_{лодки} + {V}^2_{реки}}
\end{aligned}\]МГНОВЕННАЯ И СРЕДНЯЯ СКОРОСТИ
Мгновенная скорость
Скорость точки в данный момент времени называется мгновенной скоростью.
Средняя скорость
Скорость, с которой должна двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени, называется средней скоростью перемещения.
ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ
Ускорение
Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает.
- Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.
Формула ускорения
\[\begin{aligned}\bar{a}=\frac{\bar{V_2}-\bar{V_1}}{t}, м/с^2 \end{aligned}\]- $\bar{V_2}$ - конечная скорость движения, м/с или км/ч
- $\bar{V_1}$ - начальная скорость движения, м/с или км/ч
- $t$ - прошедшее время, с или ч
Моментальная скорость точки при движении с ускорением
\[\begin{aligned}\bar{V_2}=\bar{V_1}+\bar{a}\cdot t \end{aligned}\]- $\bar{V_2}$ - конечная скорость движения, м/с или км/ч
- $\bar{V_1}$ - начальная скорость движения, м/с или км/ч
- $\bar{a}$ - ускорение, м/с2 или км/ч2
- $t$ - прошедшее время, с или ч
Положение точки при движении с ускорением
\[\begin{aligned}x_2 = x_1 + \bar{V_1}\cdot t + \frac{\bar{a}\cdot t^2}{2} \end{aligned}\]- $x_2$ - текущее положение точки
- $x_1$ - начальное положение точки
- $\bar{V_1}$ - начальная скорость движения, м/с или км/ч
- $\bar{a}$ - ускорение, м/с2 или км/ч2
- $t$ - прошедшее время, с или ч
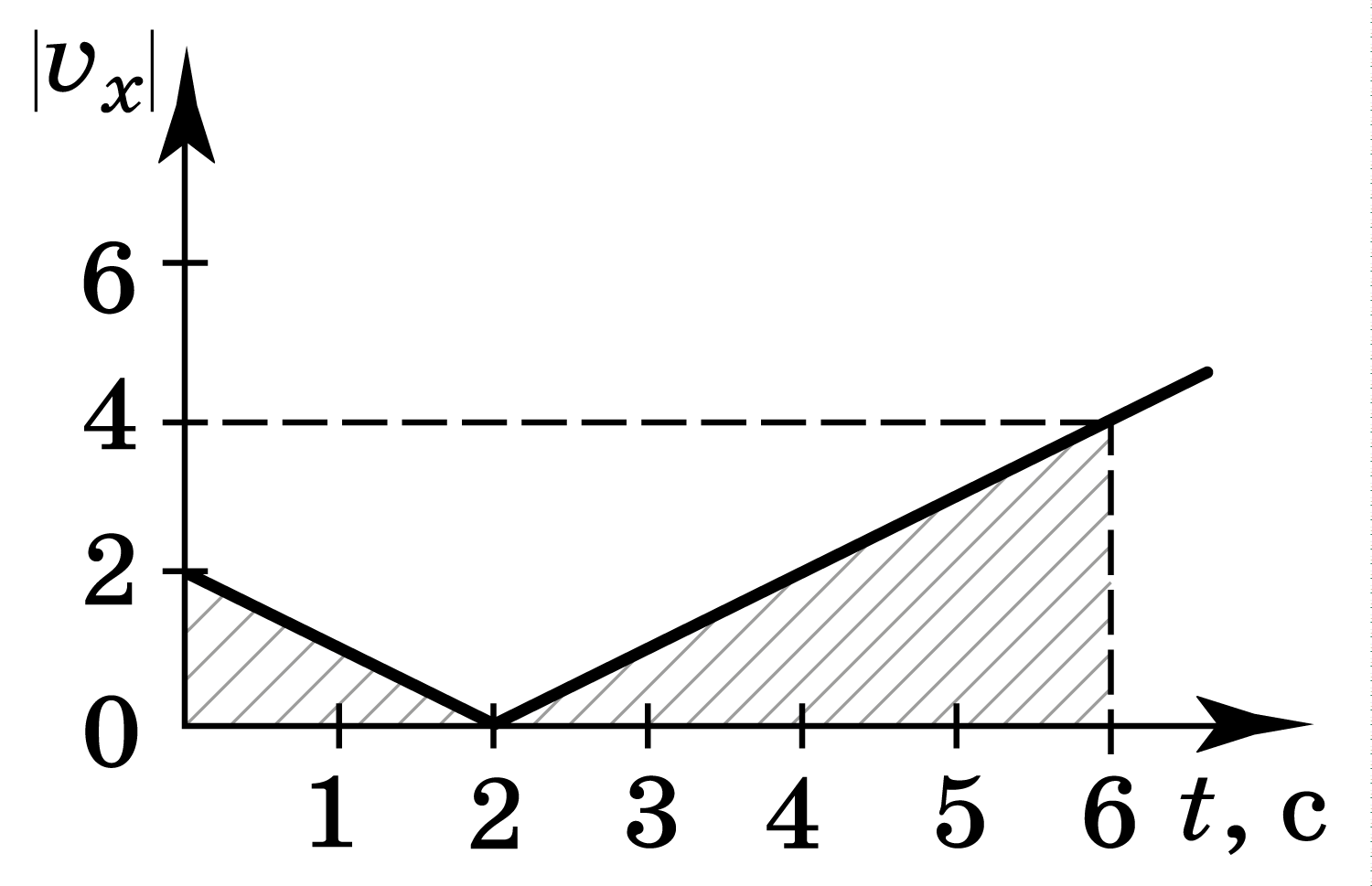
График изменения скорости со временем
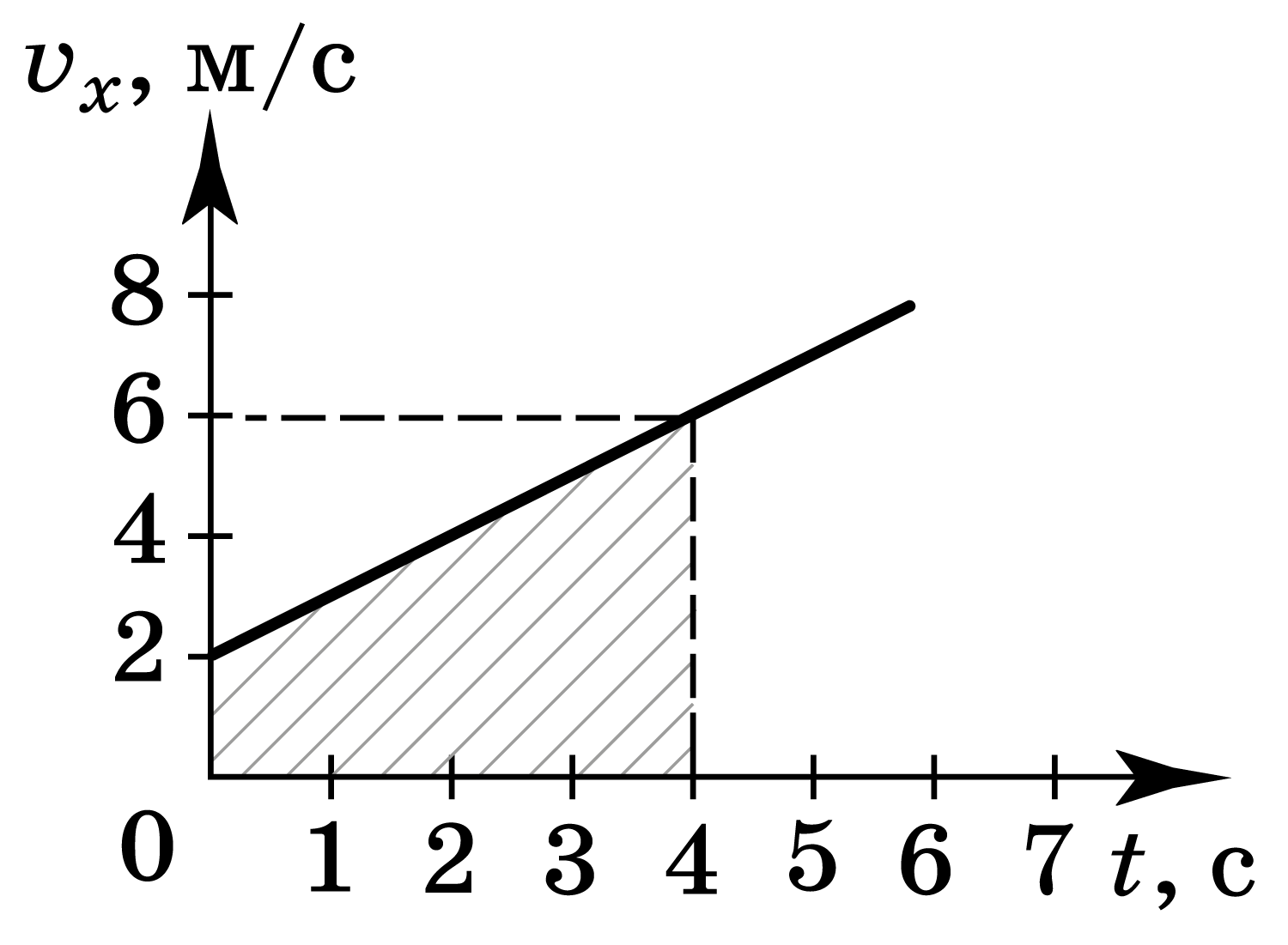
График изменения скорости со временем
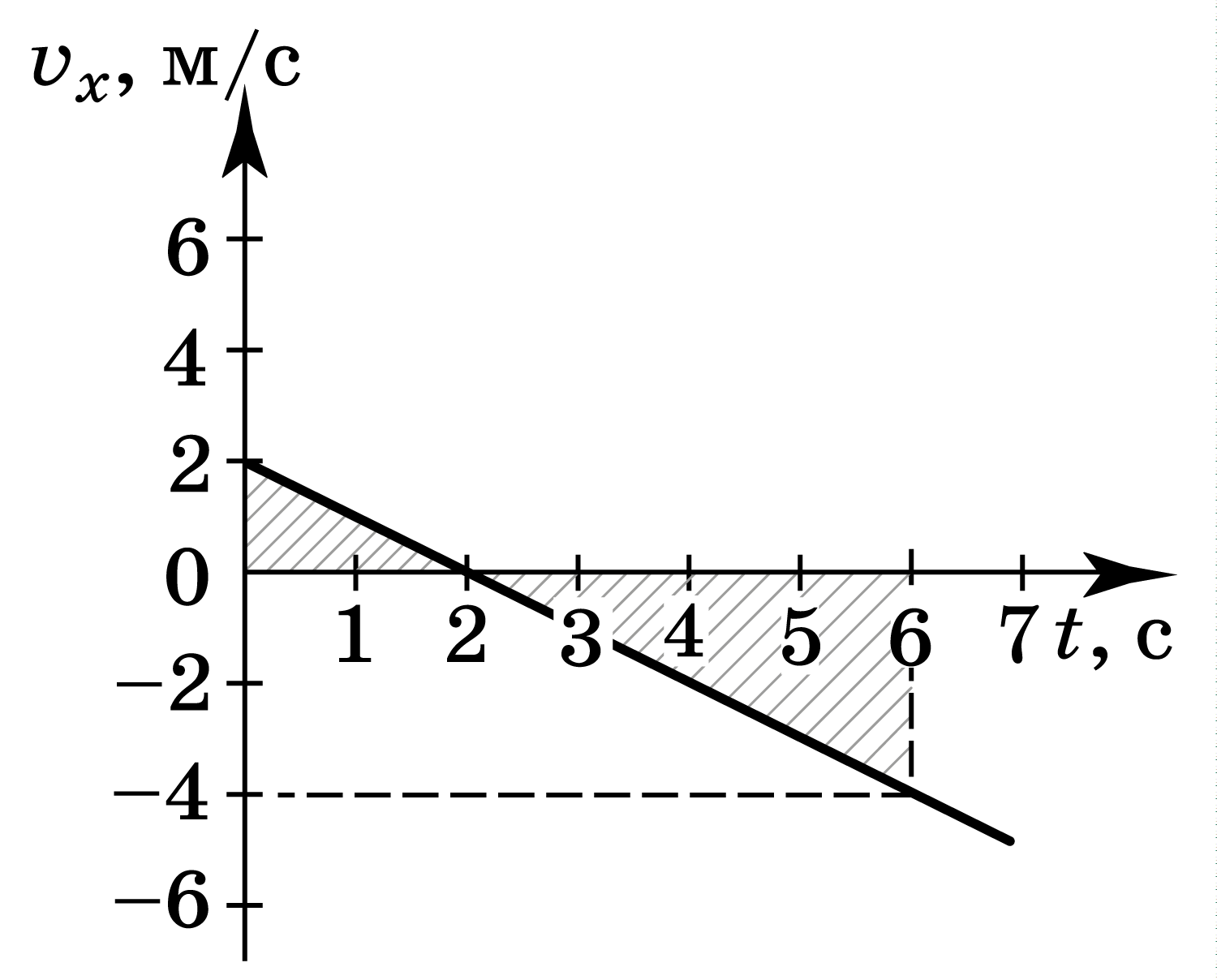
График изменения скорости со временем
